
Zadanie Najdzielniejszy dzielnik (naj)
Pomóż nam usprawnić bazę zadań!
Najdzielniejszy dzielnik
Limit pamięci: 64 MB
Dana jest liczba całkowita 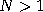 .
Powiemy, że liczba całkowita
.
Powiemy, że liczba całkowita 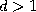 jest dzielnikiem
jest dzielnikiem 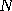 z krotnością
z krotnością 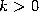 (
(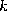 całkowite), jeżeli
całkowite), jeżeli 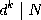 oraz
oraz 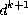 nie dzieli
nie dzieli 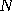 .
Dla przykładu, liczba
.
Dla przykładu, liczba 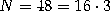 ma następujące dzielniki:
2 z krotnością 4, 3 z krotnością 1, 4 z krotnością 2, 6 z krotnością 1 itd.
ma następujące dzielniki:
2 z krotnością 4, 3 z krotnością 1, 4 z krotnością 2, 6 z krotnością 1 itd.
Powiemy, że liczba  jest najdzielniejszym dzielnikiem liczby
jest najdzielniejszym dzielnikiem liczby
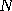 , jeżeli
, jeżeli  jest dzielnikiem
jest dzielnikiem 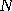 z krotnością
z krotnością 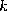 i
i 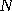 nie posiada
dzielników z krotnościami większymi niż
nie posiada
dzielników z krotnościami większymi niż 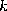 .
Przykładowo, najdzielniejszym dzielnikiem liczby 48 jest 2 (z krotnością
4), a najdzielniejszymi dzielnikami liczby 6 są: 2, 3 i 6 (każdy
z krotnością 1).
.
Przykładowo, najdzielniejszym dzielnikiem liczby 48 jest 2 (z krotnością
4), a najdzielniejszymi dzielnikami liczby 6 są: 2, 3 i 6 (każdy
z krotnością 1).
Twoim zadaniem jest wyznaczenie krotności najdzielniejszego dzielnika
liczby 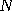 oraz wyznaczenie liczby wszystkich najdzielniejszych
dzielników
oraz wyznaczenie liczby wszystkich najdzielniejszych
dzielników 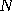 .
.
Wejście
Na standardowym wejściu znajduje się trochę nietypowy opis liczby 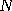 .
Pierwszy wiersz zawiera jedną liczbę całkowitą
.
Pierwszy wiersz zawiera jedną liczbę całkowitą  (
(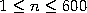 ).
Drugi wiersz zawiera
).
Drugi wiersz zawiera  liczb całkowitych
liczb całkowitych 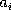 (
(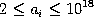 )
pooddzielanych pojedynczymi odstępami.
Opis ten oznacza, że
)
pooddzielanych pojedynczymi odstępami.
Opis ten oznacza, że 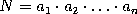 .
.
Wyjście
Pierwszy wiersz standardowego wyjścia powinien zawierać największą liczbę
całkowitą dodatnią 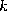 , dla której istnieje dzielnik
, dla której istnieje dzielnik  liczby
liczby 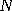 , taki
że
, taki
że 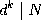 .
Drugi wiersz powinien zawierać jedną liczbę całkowitą dodatnią
.
Drugi wiersz powinien zawierać jedną liczbę całkowitą dodatnią 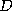 będącą
liczbą (najdzielniejszych) dzielników
będącą
liczbą (najdzielniejszych) dzielników 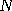 o krotności
o krotności 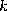 .
.
Przykład
Dla danych wejściowych:
3 4 3 4
poprawną odpowiedzią jest:
4 1
natomiast dla danych:
1 6
poprawnym wynikiem jest:
1 3
Ocenianie
Jeżeli Twój program wypisze poprawną krotność 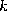 najdzielniejszego
dzielnika liczby
najdzielniejszego
dzielnika liczby 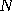 , natomiast nie wypisze w drugim wierszu liczby
najdzielniejszych dzielników
, natomiast nie wypisze w drugim wierszu liczby
najdzielniejszych dzielników 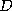 lub wypisana przez niego liczba tych
dzielników będzie niepoprawna, to uzyska 50% punktów za dany test
(oczywiście odpowiednio przeskalowane w przypadku przekroczenia połowy
limitu czasowego).
lub wypisana przez niego liczba tych
dzielników będzie niepoprawna, to uzyska 50% punktów za dany test
(oczywiście odpowiednio przeskalowane w przypadku przekroczenia połowy
limitu czasowego).
Autor zadania: Jakub Radoszewski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English